梯形面积 |
|
|
|
|
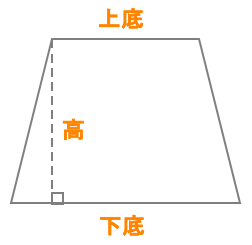
上底 下底 高 示例上底 = 4、下底 = 8、高 = 3 的梯形梯形面积 = ( 上底 + 下底 ) x 高 ÷ 2 梯形面积 = (4 + 8) x 3 ÷ 2 = 18 计算梯形的面积 |
梯形的定义梯形是具有两条平行边的四边形。梯形,也称为梯形,是具有 4 个直边的平面形状,其中有一对平行的相对边。 梯形的平行边称为梯形的底。在四边形只有一对平行边的一般情况下,这些边被称为小底和大底。 根据定义,底座是平行的。 梯形是具有恰好一对平行边的四边形。 要找到梯形的面积,请将底的总和乘以高度,然后除以 2。 梯形的面积等于高和两个底之和的乘积的一半。 梯形的性质梯形的平行边形成底边。根据定义,底座是平行的。彼此相邻的角度总和为 180°。梯形的每个下底角与同一侧的上底角互补。 等腰梯形等腰梯形(英国人称为等腰梯形)是腿全等的梯形。它就像一个等腰三角形。等腰梯形是具有一对平行边和一对全等腿的四边形。等腰梯形的底(顶部和底部)是平行的,而对边是全等的(长度相同)。 它具有全等的底角和全等的对角线。底边两边的角全等(大小相同)。 等腰梯形的对角是互补的。事实上,它们的总和是 180°。沿等腰梯形两侧的相邻角度(彼此相邻)是互补的(实际上它们的测量值加起来为 180°)。 走得更远底座(顶部和底部)彼此平行。等腰梯形的底角是全等的。 直角梯形是直角(90度)的梯形 梯形的种类等腰梯形:当它与平行边的角度相等时。等腰梯形是底角相等且左右边长也相等的梯形。直角梯形:当它有两个相邻的直角(90°)时。 不等边梯形:当梯形的边和角都不相等时,则为不等边梯形。 钝角梯形:当它的一个内角(由任一底边和一条腿形成)大于 90° 时。 锐角梯形:当它的较长底边有两个相邻的锐角时。 |